창고 다각형 ( https://www.acmicpc.net/problem/2304 )
[문제]
N 개의 막대 기둥이 일렬로 세워져 있다. 기둥들의 폭은 모두 1 m이며 높이는 다를 수 있다. 이 기둥들을 이용하여 양철로 된 창고를 제작하려고 한다. 창고에는 모든 기둥이 들어간다. 이 창고의 지붕을 다음과 같이 만든다.
- 지붕은 수평 부분과 수직 부분으로 구성되며, 모두 연결되어야 한다.
- 지붕의 수평 부분은 반드시 어떤 기둥의 윗면과 닿아야 한다.
- 지붕의 수직 부분은 반드시 어떤 기둥의 옆면과 닿아야 한다.
- 지붕의 가장자리는 땅에 닿아야 한다.
- 비가 올 때 물이 고이지 않도록 지붕의 어떤 부분도 오목하게 들어간 부분이 없어야 한다.
그림 1은 창고를 옆에서 본 모습을 그린 것이다. 이 그림에서 굵은 선으로 표시된 부분이 지붕에 해당되고, 지붕과 땅으로 둘러싸인 다각형이 창고를 옆에서 본 모습이다. 이 다각형을 창고 다각형이라고 하자.
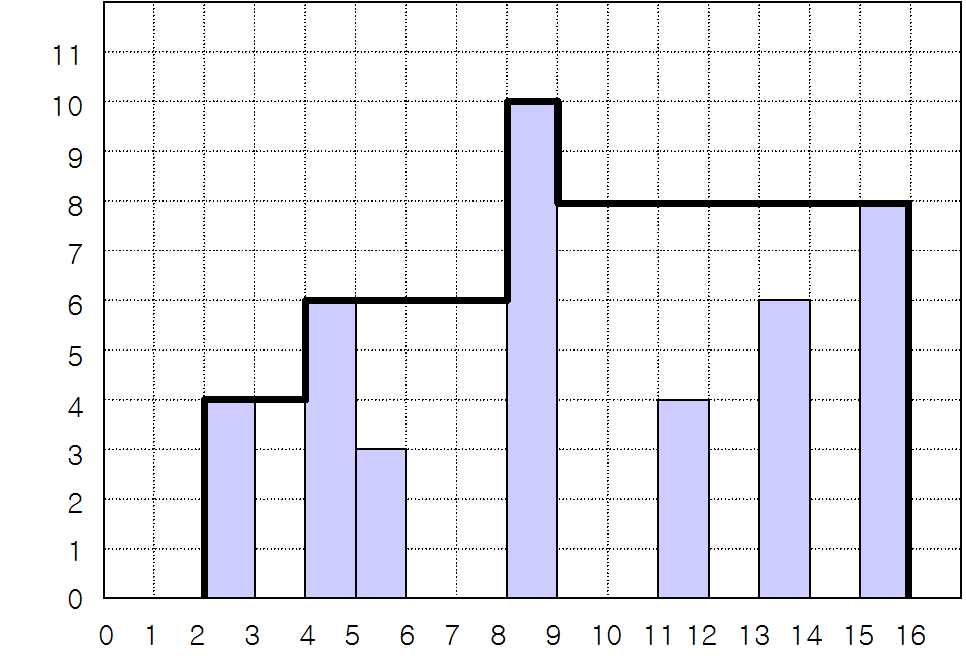
그림1 . 기둥과 지붕(굵은 선)의 예
창고 주인은 창고 다각형의 면적이 가장 작은 창고를 만들기를 원한다. 그림 1에서 창고 다각형의 면적은 98 ㎡이고, 이 경우가 가장 작은 창고 다각형이다.
기둥들의 위치와 높이가 주어질 때, 가장 작은 창고 다각형의 면적을 구하는 프로그램을 작성하시오.
[입력]
첫 줄에는 기둥의 개수를 나타내는 정수 N이 주어진다. N은 1 이상 1,000 이하이다. 그 다음 N 개의 줄에는 각 줄에 각 기둥의 왼쪽 면의 위치를 나타내는 정수 L과 높이를 나타내는 정수 H가 한 개의 빈 칸을 사이에 두고 주어진다. L과 H는 둘 다 1 이상 1,000 이하이다.
[출력]
첫 줄에 창고 다각형의 면적을 나타내는 정수를 출력한다.
[예제 입력 1]
7
2 4
11 4
15 8
4 6
5 3
8 10
13 6
[예제 출력 1]
98[체크 포인트]
1. 비가 고이지 않도록 오목한 부분이 없게 만들어야 함!
2. 왼쪽 면의 위치 앞 순서대로 차례로 최대높이를 갱신해가야함! -> sort 필요. but 최대높이 이후 낮아지는 부분 주의
[정답 코드]
# 가장 작은 창고 다각형의 면적
n = int(input()) # 기둥의 갯수
roads = [list(map(int,input().split())) for _ in range(n)]
roads.sort() # 기둥들을 x축 기준으로 정렬
result = 0
# 가장 높은 기둥의 인덱스를 알아내기(기준으로 삼을 것!)
highest_idx = 0
for i in range(n):
if road[i][1] > result:
result = road[i][1] # 가장 높은 기둥의 높이를 일단 기본값으로 두기 (해당 기둥의 높이=해당 기둥의 면적이니까!)
highest_idx = i
# 첫 번째 기둥의 높이부터 시작!
# 현재 높이 = 첫 번째 기둥의 높이 -> 높아지며 계속 갱신할 예정
height = roads[0][1]
# 최대 높이 전까지 이동하며(hightest_idx) 현재 기둥의 높이보다 다음 기둥의 높이가 더 높으면
# result에 현재까지의 면적을 계산해서 더해주고 높이를 갱신!
for i in range(highest_idx):
if height < roads[i+1][1]:
result += height * (roads[i+1][0] - roads[i][0]) # 현재의 높이 * (다음 기둥의 x값 - 현재 기둥의 x값)
height = roads[i+1][1] # 최대 높이 갱신
# 더 낮거나 같은 높이의 기둥을 만나면 현재 면적 더하기
else:
result += height * (roads[i+1][0] - roads[i][0])
#뒤에서부터도 똑같이 진행
height = roads[-1][1]
for i in range(n-1, highest_idx, -1) :
if height < roads[i-1][1] :
result += height * (roads[i][0]-roads[i-1][0])
height = roads[i-1][1]
else:
result += height * (roads[i][0] - roads[i-1][0])
print(result)[정답 해설]
먼저 해줘야될 것은 기둥들의 정보를 리스트로 받아서 x축을 기준으로 오름차순 정렬을 하는 것이다.
그리고 가장 높은 기둥을 기준으로 두 구간으로 나눠서 면적을 더해준다.
주의해야 할 것은 가장 높인 기둥의 앞쪽은 차례로 계산하면 되는데, 뒤쪽은 역으로 계산해야된다.
그렇지 않으면 그림1과 같이 가장 끝 기둥의 높이가 제일 높을 경우 오목한 부분이 생기기 때문이다.
그런데 두 구간으로 나눠지지 않는다면(가장 높은 기둥이 만약 맨첫번째 or 맨뒤라면) 두 구간으로 나눌 필요가 없으므로 예외처리를 해준다. -> 이런 식으로 if문을 넣어줬었는데 메모리, 시간을 조금이지만 더 잡아먹어서 지웠다...
if highest_idx != 0:
height = roads[0][1]
for i in range(highest_idx):
if height < roads[i+1][1]:
height = roads[i+1][1]
result += height * (roads[i+1][0] - roads[i][0])
if highest_idx != n-1:
height = roads[-1][1]
for i in range(n-1, highest_idx, -1) :
if height < roads[i-1][1] :
height = roads[i-1][1]
result += height * (roads[i][0] - roads[i-1][0])
두 구간으로 나누기 위해 기준이 되는 가장 높은 기둥의 인덱스를 구해준다.
그러면서 result에 가장 높은 기둥의 면적 (=높이*1)을 먼저 더해놓는다!
highest_idx = 0
for i in range(n):
if road[i][1] > result:
result = road[i][1]
highest_idx = i
그리고는 더 높은 기둥이 나오면 차례로 최대 높이를 계속 갱신해 갈 변수 height를 만들어준다.
오름차순이므로 초기값은 가장 첫 번째 기둥의 높이 값으로 설정한다.
height = roads[0][1]
for i in range(highest_idx):
if height < roads[i+1][1]:
result += height * (roads[i+1][0] - roads[i][0])
height = roads[i+1][1]
else:
result += height * (roads[i+1][0] - roads[i][0])
처음부터 가장 큰 기둥의 인덱스 전까지 탐색하며,
(1) height(현재까지의 최대 높이)보다 내 다음 기둥의 높이가 더 높을 경우
(내 다음 기둥의 x값 - 내 기둥의 x값) * 현재 height로 면적을 구해 더해준 다음, height를 내 다음 기둥의 높이로 갱신해준다.
(2) height(현재까지의 최대 높이)보다 내 다음 기둥의 높이가 낮거나, 같을 경우
(내 다음 기둥의 x값 - 내 기둥의 x값) * 현재 height로 면적을 구해 더해주기만 한다. 면적이 줄어들지 않고 유지되기 때문.
가장 큰 기둥의 앞쪽 면적을 구했으므로 똑같은 방식으로 뒤쪽을 구해준다. (역순)
height = roads[-1][1]
for i in range(n-1, highest_idx, -1) :
if height < roads[i-1][1] :
result += height * (roads[i][0] - roads[i-1][0])
height = roads[i-1][1]
else:
result += height * (roads[i][0] - roads[i-1][0])그런데 여기서 면적을 더하는 부분 중복 코드가 있는 것을 확인할 수 있다.
그렇다고 중복을 줄였다가는 큰일난다... 더 큰 값이 나왔을 경우 height를 갱신하기 전에 면적을 구해야되기 때문이다.
결국은 "가장 큰 기둥의 앞쪽 면적 + 가장 큰 기둥의 면적 + 가장 큰 기둥의 뒤쪽 면적" 이렇게 구한 셈이 된다.
'백준' 카테고리의 다른 글
| 백준 2503. 숫자 야구 (0) | 2024.10.20 |
|---|---|
| 백준 15649. N과 M (1) (0) | 2024.10.20 |
| 백준 21921. 블로그 (0) | 2024.04.17 |
| 백준 2512. 예산 (0) | 2024.04.16 |
| 백준 5073. 삼각형과 세 변 (0) | 2024.04.15 |